


Next: List of Tables
Up: Scalable Parallel Micromagnetic Solvers
Previous: C. Typical Material Parameters
Contents
- 2.1. Kuhn triangulation of a cube into six tetrahedral finite elements (exploded view) [16].
- 2.2. Hat function (linear basis function) for a triangulation in 2D.
- 3.1. Local coordinate system and various vectors required for the discretization of the boundary integral Eq. (3.47) [43].
- 5.1. Structure of the PETSc library.
- 5.2. Structure of additional libraries.
- 5.3. Coarse flow chart of the program.
- 5.4. Flow chart of the single processor initialization section.
- 5.5. Mesh partitioning of a soft magnetic nanodot for two, three, four, and ten processors, respectively. Different colors correspond to parts which are assigned to different processors.
- 5.6. Flow chart of the parallel initialization section.
- 5.7. Matrix-vector multiplication with matrix and vector elements distributed over four processors.
- 5.8. Sparsity pattern of the stiffness matrix of the nanodot model for a single processor (left) and distributed over two processors (right).
- 5.9. Solid angle of a trihedral angle made up by three faces of a tetrahedron.
- 5.10. Flow chart of the solution loop.
- 5.11. Flow chart of the final clean up section.
- 6.1. Global refinement of a ``parent'' tetrahedral finite element (thick lines) into eight ``children'' [16].
- 6.2. Barycentric coordinates in a regular tetrahedron.
- 6.3. Sparsity pattern of the interpolation matrix for graphics output.
- 6.4. RGB color intensities for data encoding and resulting color map.
- 6.5. Speedup of initialization, solution, and total execution time of the parallel energy minimization algorithm (TAO) on an AlphaServer.
- 6.6. Speedup of initialization, solution, and total execution time of the parallel time integration (PVODE) on an AlphaServer.
- 6.7. Speedup of initialization, solution, and total execution time of the parallel time integration (PVODE) on a Beowulf type AMD cluster.
- 7.1. TEM micrograph of the microstructure of a Sm(Co,Fe,Cu,Zr)
 precipitation hardened magnet. The lamella phase perpendicular to the
precipitation hardened magnet. The lamella phase perpendicular to the ![$[0001]$](img2.png) direction of the cell matrix phase gives strong contrast in this image [89].
direction of the cell matrix phase gives strong contrast in this image [89].
- 7.2. Bright field TEM micrograph of the cellular precipitation structure of a Sm(Co,Fe,Cu,Zr)
 magnet. The Sm
magnet. The Sm (Co,Fe)
(Co,Fe)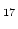 cells are surrounded by Sm(Co,Cu)
cells are surrounded by Sm(Co,Cu)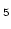 cell boundaries [89].
cell boundaries [89].
- 7.3. Lorentz electron micrograph of a Sm(Co,Fe,Cu,Zr)
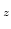 magnet. The magnetic domain wall between two domains with opposite magnetization (bright and dark cells) is pinned on the precipitation structure [87].
magnet. The magnetic domain wall between two domains with opposite magnetization (bright and dark cells) is pinned on the precipitation structure [87].
- 7.4. Model geometry for domain wall pinning on a perfectly planar interface with parallel anisotropy axes. The chain of arrows indicates the magnetization distribution of a pinned domain wall.
- . Dependence of the pinning field
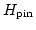 (in units of the anisotropy field of material II) on the ratio of exchange (
(in units of the anisotropy field of material II) on the ratio of exchange (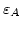 ) and anisotropy constants (
) and anisotropy constants (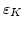 ) for given
) for given 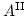 and
and
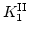 according to a 1D analytical model [91]. The thick curve represents
according to a 1D analytical model [91]. The thick curve represents
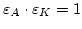 , where the two materials have equal domain wall energy and
, where the two materials have equal domain wall energy and
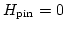 .
.
- 7.6. Model geometry for domain wall pinning on an intercellular phase with parallel anisotropy axes. The chain of arrows indicates the magnetization distribution of a pinned domain wall.
- 7.7. Pinning field for attractive and repulsive pinning as a function of the thickness
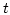 of the intercellular phase. The thickness is given in units of the exchange length of the intercellular phase. The pinning field is given in units of the pinning field for infinite
of the intercellular phase. The thickness is given in units of the exchange length of the intercellular phase. The pinning field is given in units of the pinning field for infinite 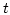 .
.
- 7.8. Model geometry for domain wall pinning on a coherent precipitation structure (with parallel anisotropy axes). The shaded areas indicate the faces of the cells, where the magnetic domain wall gets pinned.
- 7.9. Pinning field for attractive and repulsive pinning of a magnetic domain wall on the cell structure as a function of the relative thickness
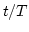 . The data marked ``area x2'' and ``area x3'' have been obtained with a model scaled to twice and three times the initial size. The dashed line is just a guide to the eye.
. The data marked ``area x2'' and ``area x3'' have been obtained with a model scaled to twice and three times the initial size. The dashed line is just a guide to the eye.
- 7.10. Domain wall energy as a function of the average edge length of the finite element model. The average edge length is given in units of the exchange length. The solid line indicates the analytical Bloch wall energy
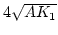 .
.
- 7.11. Demagnetization curves for different average edge length of the finite element model. The analytical pinning field has been calculated with the model presented in Sec. 7.3.1.
- 7.12. Pinning fields for different average edge length of the finite element model. As the mesh size increases the domain wall gets artificially pinned on the finite element mesh.
- 7.13. Finite element model of the rhomboidal cell structure of precipitation hardened Sm(Co,Fe,Cu,Zr)
 magnets.
magnets.
- 7.14. Demagnetization curves for reduced magnetocrystalline anisotropy
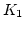 of the cell boundary phase (values in the legend in MJ/m
of the cell boundary phase (values in the legend in MJ/m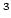 ) - attractive pinning.
) - attractive pinning.
- 7.15. Demagnetization curves for enhanced magnetocrystalline anisotropy
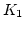 of the cell boundary phase (values in the legend in MJ/m
of the cell boundary phase (values in the legend in MJ/m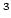 ) - repulsive pinning.
) - repulsive pinning.
- 7.16. Pinning field vs. difference in anisotropy constant between the cells and the cell boundary phase in a 3D model of the rhomboidal SmCo microstructure and comparison with the analytical 1D model of Kronmüller, Goll [91].
- 7.17. Finite element model with
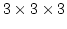 cells.
cells.
- 7.18. Domain wall bending of a magnetic domain wall in the (softer) intercellular phase (attractive pinning).
- 7.19. Demagnetization curves for varying thickness
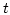 (values in the legend in nm) of the intercellular phase around large cells with
(values in the legend in nm) of the intercellular phase around large cells with
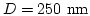 .
.
- . Magnetization distribution for
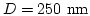 and
and
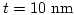 . The green surface indicates the domain wall, which separates the two domains (red and blue areas) with antiparallel magnetization.
. The green surface indicates the domain wall, which separates the two domains (red and blue areas) with antiparallel magnetization.
- . Magnetization distribution for
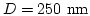 and
and
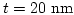 .
The green surface indicates the domain wall, which separates the two domains (red and blue areas) with antiparallel magnetization.
.
The green surface indicates the domain wall, which separates the two domains (red and blue areas) with antiparallel magnetization.
- 8.1. TEM image and material properties of FePt [100]
- 8.2. FePt nanoparticle with different easy axes [101] and FE model
- 8.3. Nucleation field of an FePt nanoparticle with uniaxial magnetocrystalline anisotropy as a function of the angle of the applied field with respect to the easy axis. The finite element simulation gives the correct result of a Stoner-Wohlfarth particle. If the demagnetizing field is taken into account, the nucleation field is reduced by less than 5 % due to the dominating high magnetocrystalline anisotropy.
- 8.4. The
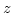 -component of the demagnetizing field has been measured along the
-component of the demagnetizing field has been measured along the 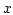 -axis through the center of the nanoparticle as shown in the left image. The result is shown in the graph on the right.
-axis through the center of the nanoparticle as shown in the left image. The result is shown in the graph on the right.
- 8.5. The
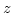 -component of the demagnetizing field has been measured along the
-component of the demagnetizing field has been measured along the 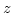 -axis through the center of the nanoparticle as shown in the left image. The result is shown in the graph on the right.
-axis through the center of the nanoparticle as shown in the left image. The result is shown in the graph on the right.
- 8.6. The
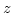 -component of the demagnetizing field has been measured along a line parallel to the
-component of the demagnetizing field has been measured along a line parallel to the 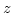 -axis close to an edge of the nanoparticle as shown in the left image. The result is shown in the graph on the right.
-axis close to an edge of the nanoparticle as shown in the left image. The result is shown in the graph on the right.
- 8.7. Coercivity as a function of the easy axis distribution and edge length of the nanoparticle. The easy axis distribution is shown in the top left figure for the ``3 easy axes'' (where two neighboring parts of the model have the same easy axis) and on the top right for the ``6 easy axes'' (where all neighboring pairs have perpendicular easy axes) distribution, respectively.
- 9.1. MFM image of nanodots with 50 nm thickness and different diameters (0.3 to 1
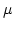 m) [107]. The dark spots in the center of the dots indicate the magnetic vortex core, where the MFM detects the stray field caused by the perpendicular magnetization.
m) [107]. The dark spots in the center of the dots indicate the magnetic vortex core, where the MFM detects the stray field caused by the perpendicular magnetization.
- 9.2. Geometry of a flat cylindrical nanodot.
- 9.3. Magnetization distribution of the vortex state on the coarse mesh. The vortex core cannot be resolved.
- 9.4. Magnetization distribution of the vortex state on the fine mesh. The vortex core is properly resolved.
- 9.5. Magnetization distribution of the vortex state on the adapted mesh. The vortex core is nicely resolved, but the total number of elements and vertices is similar to that of the coarse mesh.
- 9.6. Profile of
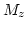 along the
along the 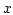 -axis through the center of the nanodot for different meshes.
-axis through the center of the nanodot for different meshes.
- 9.7. Isovolume (
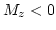 ) plot of the vortex core.
) plot of the vortex core.
- 9.8. Profiles of
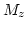 along the
along the 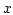 -axis through the center of the nanodot for the analytical model, its finite element approximation, and the relaxed magnetization in equilibrium.
-axis through the center of the nanodot for the analytical model, its finite element approximation, and the relaxed magnetization in equilibrium.
- . Hysteresis curve of a nanodot with
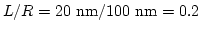 for an in-plane external
field. The circles mark the position on the hysteresis curve at
which the snapshots in Fig. 9.10 have
been taken.
for an in-plane external
field. The circles mark the position on the hysteresis curve at
which the snapshots in Fig. 9.10 have
been taken.
- 9.10. Typical magnetization distributions along the hysteresis loop. The snapshots have been taken at the corresponding position on the hysteresis curve indicated in Fig. 9.9.
- 9.11. Total energy as a function of the external field for both branches (solid line for decreasing field - dashed line for increasing field) of the hysteresis loop.
- 9.12. Exchange and magnetostatic energy and their sum as a function of the external field (for decreasing external field).
- 9.13. Hysteresis curve of a nanodot with a radius of 200 nm and a thickness of 40 nm.
- 9.14. Profiles of
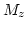 along the
along the 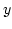 -axis through the center of the nanodot for a vortex moving in
-axis through the center of the nanodot for a vortex moving in 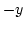 direction due to an external field increasing in
direction due to an external field increasing in 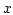 direction.
direction.
- . Comparison of
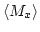 as a function of the vortex displacement between the FE simulation and the rigid vortex model.
as a function of the vortex displacement between the FE simulation and the rigid vortex model. 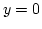 corresponds to a centered vortex,
corresponds to a centered vortex, 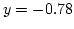 is the maximum shift before vortex annihilation occurs in the FE simulation.
is the maximum shift before vortex annihilation occurs in the FE simulation.
- 9.16. Contour plot of the surface charge density on the nanodot in zero field. Green indicates no surface charges, blue indicates negative surface charges.
- 9.17. Contour plot of the surface charge density on the circumference of the nanodot in zero field.
- 9.18. Contour plot of the surface charge density on the nanodot in an external field. Blue indicates negative charges, green zero charges, and red positive surface charges.
- 9.19. Contour plot of the surface charge density on the circumference of the nanodot in an external field.
- 9.20. Surface charge density on the circumference of the nanodot for different applied fields.
- . Surface charge distribution as a function of the polar angle on the circumference of the nanodot for different vortex shifts (indicated by different
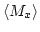 ).
).
- 9.22. Surface charge distribution on the circumference of the nanodot as a function of the polar angle. An in-plane external field shifts the vortex (cf. Fig. 9.23) and leads to surface charges on the circumference. The rigid vortex model (gray lines) overestimates the charge density as compared to the FE simulation (black lines).
- . Contour plot of
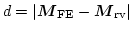 . Blue areas indicate good agreement of the magnetization distribution between the rigid vortex model (black cones) and the FE model (gray cones), red areas indicate larger differences.
. Blue areas indicate good agreement of the magnetization distribution between the rigid vortex model (black cones) and the FE model (gray cones), red areas indicate larger differences.
- .
 and
and
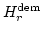 across the nanodot.
across the nanodot.
- 9.25. Phase diagram of magnetic ground states of magnetic nanodots.
- 9.26. Equilibrium magnetization distributions in zero field inside the nanodots (cut along the cylinder axis) for dots with aspect ratios
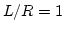 .
.
- 9.27. Magnetization distributions for dots with aspect ratios
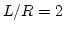 .
.
- . Oscillation of
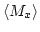 as the vortex core precesses towards equilibrium.
as the vortex core precesses towards equilibrium.
- . Oscillation of
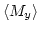 as the vortex core precesses towards equilibrium.
as the vortex core precesses towards equilibrium.
- 9.30. Oscillation of the magnetostatic energy.
- . Simulation results for vortex precession in a nanodot with
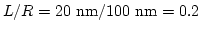 under applied in-plane field
under applied in-plane field
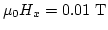 .
.
- 9.32. Translation mode eigenfrequencies versus aspect ratio
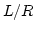 for nanodots with
for nanodots with
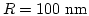 .
.
- 9.33. Energy over time for a dot with
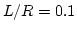 and
and
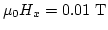 .
.
- 9.34. Snapshots of
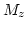 as a function of the radius at different times during one oscillation period. The magnetization fluctuation outside the vortex core is very uniform, while the vortex core remains undisturbed (``rigid'').
as a function of the radius at different times during one oscillation period. The magnetization fluctuation outside the vortex core is very uniform, while the vortex core remains undisturbed (``rigid'').
- 9.35.
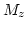 as a function of time at different radii. The magnetization is perfectly in phase in all spots, which emphasizes the uniformity of the excitation mode.
as a function of time at different radii. The magnetization is perfectly in phase in all spots, which emphasizes the uniformity of the excitation mode.
- 9.36. Fourier spectrum of
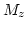 (of Fig. 9.35) at different radii.
(of Fig. 9.35) at different radii.
- 9.37.
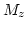 as a function of time at
as a function of time at 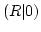 and
and 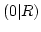 .
.
- 9.38. Fourier spectrum of
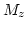 (of Fig. 9.37) at
(of Fig. 9.37) at 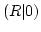 and
and 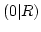 .
.
- 9.39.
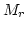 as a function of the radius at different
as a function of the radius at different 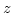 positions.
positions.
- 9.40.
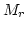 as a function of the radius at different times.
as a function of the radius at different times.
- 9.41.
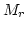 and
and 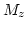 as a function of time at different radii.
as a function of time at different radii.
- 9.42. Fourier spectrum of
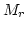 and
and 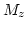 (of Fig. 9.41) at different radii.
(of Fig. 9.41) at different radii.
- 9.43.
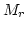 as a function of time at
as a function of time at 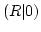 and
and 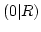 .
.
- 9.44. Fourier spectrum of
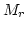 (of Fig. 9.43) at
(of Fig. 9.43) at 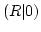 and
and 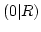 .
.
- 9.45.
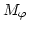 as a function of the radius at different times.
as a function of the radius at different times.
- 9.46.
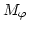 as a function of time at different radii.
as a function of time at different radii.
- 9.47. Simulation results for a nanodot with
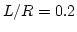 under applied out-of-plane field
under applied out-of-plane field
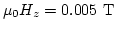 .
.
- . Simulation results for a nanodot with
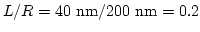 .
.
- 10.1. Shape and finite element mesh of an elliptical nanoparticle.
- 10.2. Snapshot of the magnetization reversal process of a single particle.
- 10.3. Snapshot of the magnetization reversal process of a chain of six elliptical particles.
- 10.4. Demagnetization curves for a chain of elliptical and rectangular particles with parallel and antiparallel initial magnetization.
- 10.5. Snapshot of the magnetization reversal process of a chain of six rectangular particles.
- 10.6. Chain of particles with the initial magnetization parallel to the chain axis.
- 10.7. Snapshot of the relaxation process of a chain of six elliptical and rectangular particles with their initial magnetization parallel to the chain axis.
- 10.8. Equilibrium magnetization distribution in zero field of a chain of six elliptical and rectangular particles with their initial magnetization parallel to the chain axis.
- 10.9. Demagnetization curves for a chain of elliptical particles with (``touch.'' -
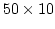 nm) and without (``isol.'') contact faces with parallel and antiparallel initial magnetization.
nm) and without (``isol.'') contact faces with parallel and antiparallel initial magnetization.
- 10.10. Equilibrium magnetization distribution in zero field of a chain of 6 elliptical particles with a contact area of
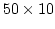 nm.
nm.
- 10.11. Demagnetization curves for a chain of elliptical particles with (``touch.'' -
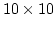 nm) and without (``isol.'') contact faces with parallel and antiparallel initial magnetization.
nm) and without (``isol.'') contact faces with parallel and antiparallel initial magnetization.
- 10.12. Equilibrium magnetization distribution in zero field of a chain of six elliptical particles with a contact area of
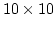 nm.
nm.
- 10.13. Demagnetization curves for a chain of elliptical particles with
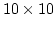 nm and
nm and 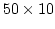 nm contact faces with parallel and antiparallel initial magnetization.
nm contact faces with parallel and antiparallel initial magnetization.
Werner Scholz
2003-06-08