9.3 Static Properties

First we have investigated the static properties of the permalloy nanodots and compared the results of the analytical rigid vortex model and the numerical finite element simulations.

The finite element simulations have been initialized with the magnetization distribution of the rigid vortex model and an approximate core radius. Then the Landau-Lifshitz equation of motion for the magnetization has been integrated with a damping constant 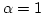$\alpha =1$ in zero field, and the magnetization relaxed to its equilibrium distribution, which minimizes the total Gibbs free energy.

For the coarse mesh the magnetization distribution given in Fig. 9.3 has been found.

Figure 9.3: Magnetization distribution of the vortex state on the coarse mesh. The vortex core cannot be resolved.

Obviously, the resolution of the mesh is too low to properly resolve the vortex. Thus, 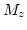$M_z$ is zero in the whole dot. The second mesh with a mesh size of 0.06 is fine enough to resolve the core (Fig. 9.4).

Figure 9.4: Magnetization distribution of the vortex state on the fine mesh. The vortex core is properly resolved.

The adapted mesh, which has a high resolution with many small elements in its center and a gradually decreasing resolution towards the circumference, resolves the core just as well as the fine mesh (cf. Fig. 9.5), but its number of nodes and elements is comparable to that of the coarse mesh. Therefore it is very well suited for simulations, where the vortex core can be expected to be in the center of the nanodot. If the vortex core moves out of the center (e.g. due to an external field), it might reach a region with a low resolution mesh. Then, the vortex core cannot be resolved properly any more and the results become very unreliable. As a result, it is necessary to use either a uniform high resolution mesh or to apply adaptive mesh refinement, which increases the mesh density at run time as required and optimizes (minimizes) the number of nodes and elements in the finite element mesh.

Figure 9.5: Magnetization distribution of the vortex state on the adapted mesh. The vortex core is nicely resolved, but the total number of elements and vertices is similar to that of the coarse mesh.

The profile of 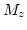$M_z$ along the 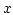$x$-axis through the center of the dot for the different meshes is given in Fig. 9.6.

Figure 9.6: Profile of 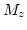$M_z$ along the 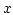$x$-axis through the center of the nanodot for different meshes.

The coarse grid clearly fails to resolve the vortex. However, the fine and the adapted grid are in excellent agreement. This emphasizes the importance of suitable meshing, because the fine grid consists of more than four times more elements than the adapted one, which leads to much longer computation times. However, if we define the vortex core radius as that radius, where 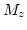$M_z$ is zero, we find a value of approximately 25 nm, which is considerably larger than the value predicted by the rigid vortex model (11 nm, see above). 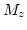$M_z$ is also quite uniform across the thickness of the dot. This fact and the ``shape'' of the vortex core are visualized in Fig. 9.7. The core is plotted as the isovolume, where 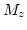$M_z$ is 0 or lower (the vortex is pointing in 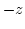$-z$ direction). This corresponds to the definition of the rigid vortex model. The dot itself is sketched by the edges of its top and bottom surface.

Figure 9.7: Isovolume (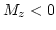$M_z < 0$) plot of the vortex core.