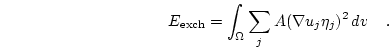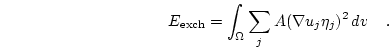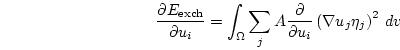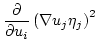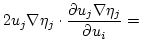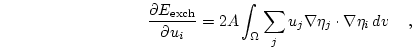


Next: 3.3.2 Magnetocrystalline Anisotropy Energy
Up: 3.3 Discretization
Previous: 3.3 Discretization
Contents
The exchange energy for one Cartesian component is given by
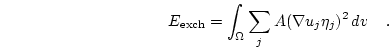 |
(3.15) |
For the gradient we obtain
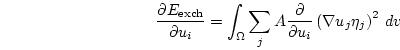 |
(3.16) |
Finally, the gradient of the exchange energy is given by
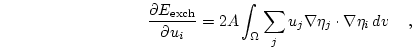 |
(3.20) |
which can be written as a linear system of equations with the coefficient matrix
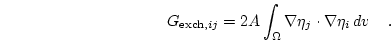 |
(3.21) |
The gradient can then be simply calculated as
 |
(3.22) |
The expressions for the 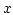 ,
, 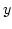 , and
, and 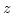 -component are identical and there are no mixed terms.
-component are identical and there are no mixed terms.
This exchange energy matrix is proportional to the stiffness matrix of the Laplacian operator Eq. (2.15), which is also obvious from Brown's equation Eq. (3.4) and the effective field Eq. (3.5).



Next: 3.3.2 Magnetocrystalline Anisotropy Energy
Up: 3.3 Discretization
Previous: 3.3 Discretization
Contents
Werner Scholz
2003-06-08