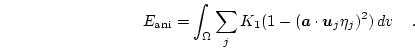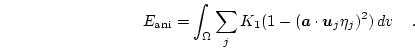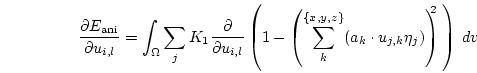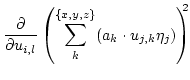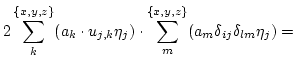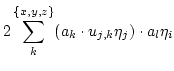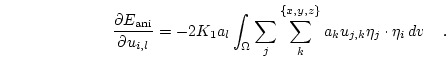


Next: 3.3.3 Zeeman Energy
Up: 3.3 Discretization
Previous: 3.3.1 Exchange Energy
Contents
The magnetocrystalline anisotropy energy for uniaxial anisotropy is given by
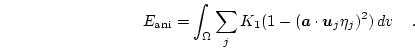 |
(3.23) |
The gradient is given by
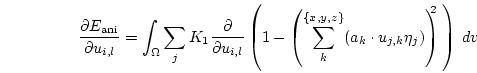 |
(3.24) |
and we get the result
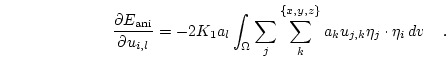 |
(3.26) |
This can be rewritten in matrix notation as
 |
(3.27) |
with
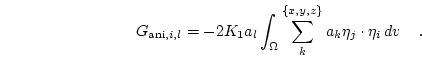 |
(3.28) |
Werner Scholz
2003-06-08