The Zeeman energy of a magnetic body
![]() in an external field
in an external field
![]() is simply given by
is simply given by
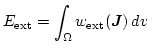 |
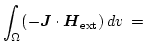 |
(3.29) | |
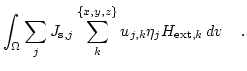 |
(3.30) |
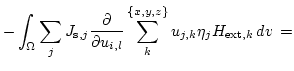 |
(3.31) | ||
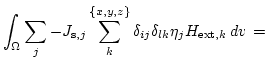 |
(3.32) | ||
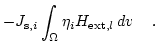 |
(3.33) |
Since we know the external field explicitly, we can just simply add it to the other contributions to the effective field.