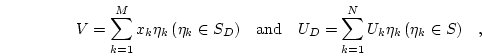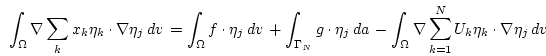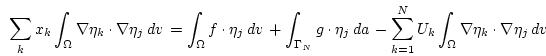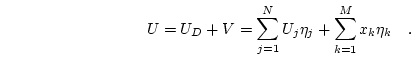


Next: 2.4 Mesh Generation
Up: 2. The Finite Element
Previous: 2.2 The Weak Formulation
Contents
2.3 Galerkin Discretization
In order to solve the Poisson problem numerically we have to discretize the weak formulation of the Poisson equation (Eq. (2.8)) and restrict the solution space of the numerical solution 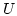 to a finite dimensional subspace
to a finite dimensional subspace 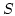 of
of 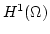 . Accordingly
. Accordingly
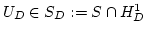 approximates
approximates 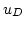 on
on  . The discretized problem
. The discretized problem 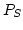 can then be written as: Find
can then be written as: Find 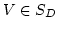 such that
such that
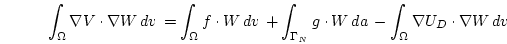 |
(2.9) |
with 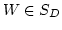 .
.
If we assume that
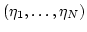 is a basis of the
is a basis of the
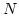 -dimensional space
-dimensional space 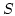 and
and
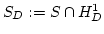 a
a 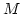 -dimensional subspace
then we can rewrite Eq. (2.9)
-dimensional subspace
then we can rewrite Eq. (2.9)
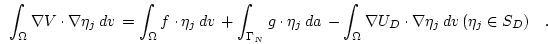 |
(2.10) |
If we now make a series expansion of 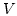 and
and 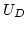 in terms of
in terms of 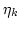
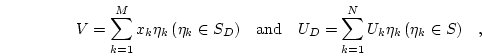 |
(2.11) |
then we obtain
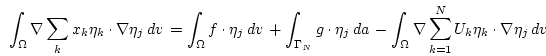 |
(2.12) |
which can be rewritten as
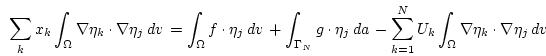 |
(2.13) |
and finally simplified to a system of linear equations
 |
(2.14) |
where the ``stiffness matrix'' is given by
 |
(2.15) |
and the ``right hand side'' by
 |
(2.16) |
The stiffness matrix is sparse, symmetric, and positive definite. Thus, Eq. (2.14) has exactly one solution
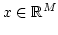 ,
which gives the Galerkin solution
,
which gives the Galerkin solution
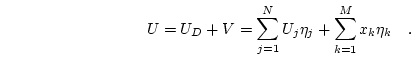 |
(2.17) |



Next: 2.4 Mesh Generation
Up: 2. The Finite Element
Previous: 2.2 The Weak Formulation
Contents
Werner Scholz
2003-06-08
![]() to a finite dimensional subspace
to a finite dimensional subspace ![]() of
of ![]() . Accordingly
. Accordingly
![]() approximates
approximates ![]() on
on ![]() . The discretized problem
. The discretized problem ![]() can then be written as: Find
can then be written as: Find ![]() such that
such that
![]() is a basis of the
is a basis of the
![]() -dimensional space
-dimensional space ![]() and
and
![]() a
a ![]() -dimensional subspace
then we can rewrite Eq. (2.9)
-dimensional subspace
then we can rewrite Eq. (2.9)