7.2.2 Milshtein scheme

The Milshtein scheme [44] is obtained by adding the term

$$b b' I_{(1,1)} = \frac{1}{2} b b' \left[ (\Delta W)^2-\Delta t \right]$$

from the Itô-Taylor expansion () to the Euler scheme ().

$$Y_{n+1}=Y_n + a \Delta t + b \Delta W + \frac{1}{2} b b' \left[ (\Delta W)^2 - \Delta t \right] \quad.$$ (7.6)

The same scheme is found for the Stratonovich interpretation from the Stratonovich-Taylor expansion () with ()

$$Y_{n+1}=Y_n + \bar a \Delta t + b \Delta W + \frac{1}{2} b b' (\Delta W)^2 \quad,$$ (7.7)

where

$$\bar a = a - \frac{1}{2} b b' \quad.$$

The addition of this term increases the order of strong convergence from 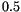$0.5$ for the Euler scheme to 1 for the Milshtein scheme. It corresponds to that of the deterministic Euler scheme without any noise, that is with $b \equiv 0$. Thus, the Milshtein scheme can be interpreted as the proper generalization of the deterministic Euler scheme for the strong order convergence criterion ().

The generalization for our multidimensional Langevin equation () gives

$$M_i(t+\Delta t) = M_i(t) + A_i(\mathbf{M}, t) \Delta t + ... ...{jk}\frac{\partial B_{ik}}{\partial M_j} (\Delta W_k)^2 \quad.$$ (7.8)

For the noise induced drift term we get

$$B_{jk}\frac{\partial B_{ik}}{\partial M_j} = \left( -\gamma'\varepsilon _{jlk} M_l % -\frac{\alpha \gamma'}{M_\mathrm{s}} ( M_j M_k % -\delta_{jk}M_\mathrm{s}^2 % ) \right)$$

$$\left( -\gamma'\varepsilon _{ijk} % -\frac{\alpha \gamma'}{M_\mathrm{s}} ( \delta_{ij}M_k + % \delta_{jk}M_i - % 2 \delta_{ik}M_j % ) \right)$$

$$= \gamma'^2 \varepsilon _{jlk}\varepsilon _{ijk} M_l + <tex2html_comment_mark>$$

$$\frac{\alpha \gamma'^2}{M_\mathrm{s}} \bigl( \varepsilon _{jlk} \... ...{jk} M_i M_l % -2\delta_{ik \varepsilon _{jlk} M_l M_j} <tex2html_comment_mark>$$

$$\qquad +\varepsilon _{ijk} M_j M_k % -\varepsilon _{ijk} \delta_{jk} M_\mathrm{s}^2 % \bigr)+$$

$$\frac{\alpha^2 \gamma'^2}{M_\mathrm{s}^2} \bigl( \delta_{ij} M_j M_k M_k % +\delta_{jk} M_i M_j M_k % -2\delta_{ik}M_k M^2 <tex2html_comment_mark>$$

$$-\delta_{jk} \delta_{ij} M_k M_\mathrm{s}^2 % -\delta_{jk} \delta_{jk} M_i M_\mathrm{s}^2 % +2\delta_{ik}\delta_{jk}M_j M^2 % \bigr)$$

$$= -\gamma'^2 2\delta_{il} M_l +\alpha^2 \gamma'^2 \left( -2\delta_{ij} M_i \right)$$

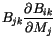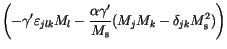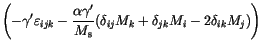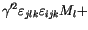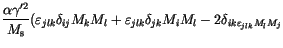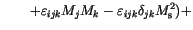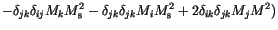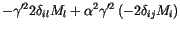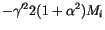$$= -\gamma'^2 2 (1+\alpha^2)M_i$$ (7.9)

The additional stochastic term of the Milshtein scheme () corresponds to the drift term of the Euler scheme in Stratonovich interpretation () [45]. In the Euler scheme this term is

$$2D\frac{1}{2} B_{jk}\frac{\partial B_{ik}}{\partial M_j} \Delta t \quad\$$

whereas in the Milshtein scheme it reads as

$$\frac{1}{2} B_{jk}\frac{\partial B_{ik}}{\partial M_j} (\Delta W_k)^2 \quad.$$

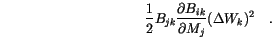
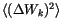So, the term $(\Delta W_k)^2$ is replaced by its mean value $\langle {(\Delta W_k)^2} \rangle$, which is 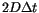$2D\Delta t$ according to (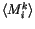). This small modification accounts for the difference in the order of convergence. However, if one is interested only in computing the moments $\langle {M_i^k} \rangle$, for example, it can be shown, that the Euler and Milshtein algorithm are of equal accuracy. However, since both algorithms have approximately the same computational complexity, it does not seem to be justified to use the poorer Euler algorithm instead of the Milshtein algorithm.