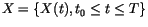7.2.1 Euler scheme

We shall consider an Itô process 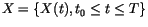$X=\{X(t), t_0 \le t \le T\}$ satisfying the scalar stochastic differential equation with multiplicative noise

$$dX(t)=a(X(t),t) \,d{t}\, + b(X(t),t) \,d{W(t)}\,$$

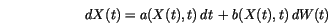
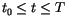on $t_0 \le t \le T$ with the initial value

$$X(t_0)=X_0 \quad.$$

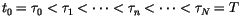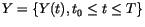For a given discretization $t_0 = \tau_0 < \tau_1 < \cdots < \tau_n < \cdots < \tau_N = T$ of the time interval $[t_0,T]$, an Euler approximation [40] is a continuous time stochastic process $Y=\{Y(t),t_0 \le t \le T\}$ satisfying the iterative scheme

$$Y_{n+1}=Y_n+a(\tau_n,Y_n) \Delta_n+ b(\tau_n,Y_n) \Delta W_n \quad,$$ (7.1)

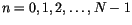for $n=0,1,2, \dots, N-1$ with initial value

$$Y_0=X_0 \quad,$$

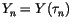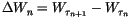where $Y_n=Y(\tau_n)$, $\Delta_n=\tau_{n+1}-\tau_n$ denotes the time discretization interval, and $\Delta W_n = W_{\tau_{n+1}}-W_{\tau_n}$ is the increment of the stochastic process.

If $b \equiv 0$, that is if the diffusion coefficient is identically zero, the stochastic iterative scheme () reduces to the deterministic Euler scheme for the ordinary differential equation

$$\frac{dx}{dt}=a(x,t) \quad.$$

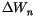The random increments $\Delta W_n$ are independent Gaussian random variables with mean

$$\langle {\Delta W_n} \rangle =0$$

and variance

$$\langle {(\Delta W_n)^2} \rangle =\tau_{n+1}-\tau_n \quad.$$ (7.2)

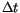For the integration of the Langevin equation () with constant step size $\Delta t$ the Euler scheme results in

$$M_i = M_i(t) + A_i(\mathbf{M}, t)\Delta t + B_{ik}(\mathbf{M}, t)\Delta W_k$$ (7.3)

with

$$\langle {\Delta W_k} \rangle =0 \, , \quad \langle {\Delta W_k \Delta W_l} \rangle = 2 D \delta_{kl} \Delta t \quad.$$

In the context of Stratonovich stochastic calculus the deterministic drift has to be augmented by a noise induced drift term () which gives

$$M_i(t+\Delta t) = M_i(t) + \left[ A_i(\mathbf{M}, t) + 2... ...j} \right] \Delta t + B_{ik}(\mathbf{M}, t)\Delta W_k \quad.$$ (7.4)

However, in the presence of the stochastic term the order of convergence of the stochastic Euler scheme is lower than that of the deterministic scheme.

A time discrete approximation 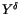$Y^\delta$ with maximum step size 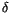$\delta$ converges strongly to 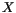$X$ at time 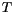$T$ if

$$\lim_{\delta \downarrow 0} \langle {\vert X(T)-Y^\delta(T)\vert} \rangle =0 \quad.$$

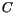If there exists a positive constant $C$, which does not depend on 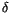$\delta$, and a 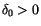$\delta_0 > 0$ such that

$$\langle {\vert X(T)-Y^\delta(T)\vert} \rangle \le C \delta^\gamma$$ (7.5)

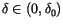for each $\delta \in (0,\delta_0)$, the time discrete approximation 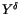$Y^\delta$ is said to converge strongly with order 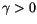$\gamma > 0$ at time $T$.

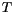If the drift and diffusion coefficients are almost constant, the Euler scheme gives good numerical results. In practice this is rarely the case and then the results can become very poor, because it converges with an order of 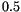$0.5$ only [40]. (Notice, that the corresponding deterministic scheme has an order of 1.) Therefore, it is recommended to use higher order schemes.