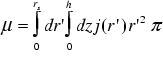 (
( 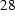 )
)
In order to calculate the magnetic moment, which is caused by the circular eddy currents, we have to integrate the eddy current density over the volume of the cylindrical samples (radius rs, height h).
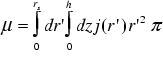 (
( 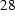 )
)
We have seen in figure 19, that the eddy current density is directly proportional to the radial distance from the symmetry axis. Thus, we write
 . (
. ( 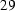 )
)
We obtain for the magnetic moment
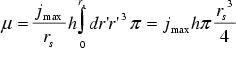 . (
. ( 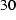 )
)
The magnetization is given by
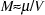 , (
, ( 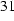 )
)
where V is the volume of our cylinders
 (
( 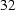 )
)
Finally, we find for the magnetization
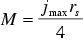 . (
. ( 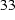 )
)
Hence, the magnetization is independent of the height of the cylinder.
Since our samples have a radius rs of 2 mm we get
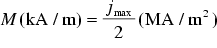 . (
. (  )
)
In order to calculate the magnetic moment of the spherical samples, we have to integrate the eddy current density over the volume of the sphere (radius r).
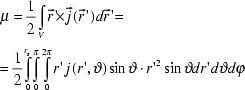 (
(  )
)
We have seen in figure 20, that the eddy current density is also in spherical samples directly proportional to the radial distance from the symmetry axis. Thus, we write
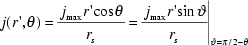 . (
. ( 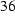 )
)
We obtain for the magnetic moment
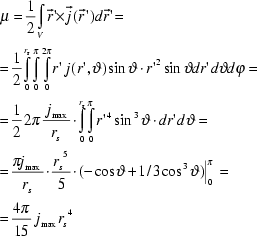 . (
. (  )
)
The magnetization is given by
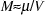 , (
, (  )
)
where V is the volume of our cylinders
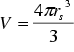 (
(  )
)
Finally, we find for the magnetization
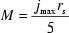 . (
. (  )
)
![]()
![]()
![]()
![]()
Next: Eddy currents in a solid sphere
Up: Calculation of eddy currents
Previous: Eddy currents
Contents