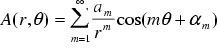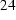For the solution of partial differential equations like Maxwell's equations, we need boundary conditions to find a unique solution. There are three types of boundary conditions:
Dirichlet boundary conditions
The value of the solution is explicitly defined on the boundary (or part of it). The magnetic vector potential is usually set to zero along a boundary, which should not be crossed by magnetic flux.
Neumann boundary conditions
The normal derivative of the solution is defined on the boundary. If we set the normal derivative of the magnetic vector potential to zero, the boundary can be interpreted as an interface with a highly permeable metal. Then, the magnetic flux passes the interface at an angle of 90° to the plane of the interface. In order to find a unique solution, a Dirichlet boundary condition must be defined somewhere on the boundary of the domain.
Robin boundary conditions
A combination of the first two boundary conditions is called a Robin boundary condition. In this case the normal derivative of the solution and the value of the solution itself on the boundary are connected by a function.
Asymptotic boundary conditions
For many problems neither of the two boundary conditions above is suitable: Natural boundary conditions usually set the solution to a distinct value at infinity. However, finite element methods, can only handle finite domains to solve the problem in a computer at finite speed with finite memory.
One workaround is the truncation of outer boundaries. At an arbitrary distance "far enough away" from the area of interest Dirichlet or Neumann boundary conditions are applied. This is very simple, but not very accurate. In addition, it is quite inefficient, because a volume of air, which is much larger than the area of interest, has to be modeled. A fine mesh in the area of interest and a coarse mesh in the exterior can reduce the computational effort again.
Asymptotic boundary conditions transform natural boundary conditions into Robin boundary conditions on the surface of a finite domain. This is achieved by developing the solution into a series expansion of spherical harmonics.
( 
)
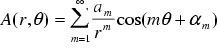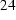Only the leading harmonic
( 
)
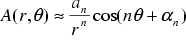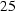is considered, since higher order harmonics decay very quickly.
We get the normal derivative on a spherical surface by differentiating with respect to r. Solving for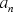 
and substituting into (25) gives
( 
)
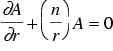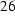If the outer edge of the solution domain is circular the open domain solution can be closely approximated by applying (26) at the boundary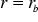 
, which should be at least 5 times the radius of the area of interest.
Next: FEMM
Up: Calculation of eddy currents
Previous: The finite element method
Contents