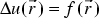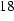The finite element method has become a well established method in many fields of computer aided engineering, such as structural analysis, fluid dynamics, and electromagnetic field computation.
There are tree main steps during the solution of a partial differential equation (PDE) with the finite element method. First, the domain, on which the PDE should be solved, is discretized into finite elements. Depending on the dimension of the problem this can be triangles, squares, rectangles, or tetrahedrons, cubes, or hexahedrons. The solution of the PDE is approximated by piecewise continuous polynomials and the PDE hereby discretized and split into a finite number of algebraic equations. Thus, the aim is to determine the unknown coefficients of these polynomials in such a way, that distance (which is defined by the norm in a suitable vector space) from the exact solution becomes a minimum. Therefore, the finite element method is essentially a variational minimization technique.
Since the number of elements is finite, we have reduced the problem of finding a continuous solution for our PDE to calculating the finite number of coefficients of the polynomials.
The solution of Poisson's equation (17), which is required to calculate the magnetic vector potential, has to be solved for a given current density distribution. We write Poisson's equation in a more general form
. ( 
)
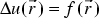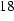In order to apply the finite element method, we have to find a variational formulation.
The Galerkin method leads to the weak formulation of the problem: We multiply Poisson's equation by a test function v( r) and integrate over the solution domain
. ( 
)
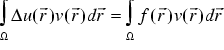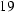Integration by parts gives
. ( 
)
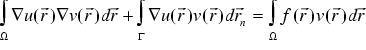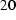where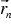 
denotes the surface normal on the boundary 
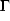. If appropriate boundary conditions define the values of u(Dirichlet boundary conditions) or of its derivatives 
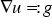(Neumann boundary conditions) on the boundary, we can simplify (since v vanishes, where Dirichlet boundary conditions apply)
. ( 
)
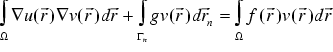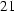The exact solution u( r) shall be approximated by a linear combination of trial functions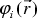 
. ( 
)
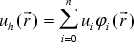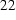and we use a finite set of test functions vi.
If we insert this expansion in (21) and assume only Dirichlet boundary conditions
. ( 
)
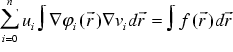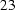we get a system of algebraic equations.
This can be solved with any standard method for the solution of a system of algebraic equations, such as the Gauß method, the Cholesky decomposition or iterative schemes like the conjugate gradient method.
Next: Boundary Conditions
Up: Calculation of eddy currents
Previous: Maxwell's equations
Contents