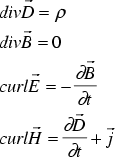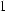Until the 19th century electric and magnetic effects were seen as two independent physical occurences. In 1820 Oersted proved, that electric currents can influence the needle of a compass. Ampère and Faraday laid the foundation for the unified theory of electrodynamics, which was elaborated by James Clerk Maxwell (1831-1879).
His famous equations are the starting point for our investigations:
( 
)
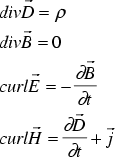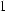In order to solve these equations for our purpose, we have to make several assumptions. First, we neglect any displacement currents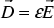 
, which are typically relevant only at radio frequencies (in the MHz regime), and set 
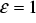. In the quasistatic approximation we omit the the term
( 
)
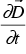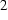Secondly, we assume, that there are no free charges (. The simplified Maxwell equations are given by
( 
)
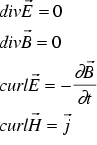Then, we require the field intensity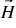 
and the flux intensity 
to obey the constitutive relationship
. ( 
)
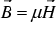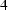If the material is nonlinear (e.g. ferromagnetic), the permeability ( is a function of B.
( 
)
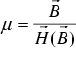However, we will consider only linear materials in this case in this project.
The relationship between the electric field intensity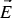 
and the current density 
is given by
. ( 
)
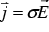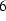Now we introduce a magnetic vector potential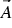 
, and define it as
( 
)
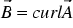which guarantees the validity of Maxwell's second equation. Then we can rewrite the fourth equation and obtain
( 
)
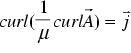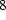With the Coulomb gauge condition
( 
)
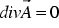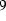and the well known operator relation
( 
)
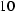we find
. ( 
)
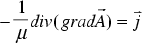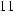Inserting (7) in the third Maxwell equation yields
. ( 
)
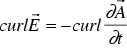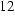In the case of 2D problems, we can integrate this equation and get
( 
)
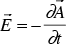and together with constitutive relationship between the electric field intensity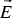 
and the current density 
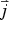we obtain
( 
)
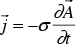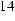Finally we insert this in (11) to eliminate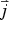 
and arrive at
, ( 
)
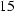where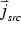 
represents the applied current sources.
Finally, we restrict ourselves to time harmonic problems, in which all fields oscillate harmonically at one fixed frequency. Thus, we can use a phasor transformation and rewrite the magnetic vector potential as
( 
)
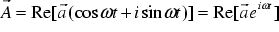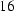in which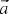 
is the complex amplitude. By substituting this ansatz in (15) we can eliminate the time derivative and finally arrive at
. ( 
)
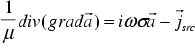Next: The finite element method
Up: Calculation of eddy currents
Previous: Calculation of eddy currents
Contents