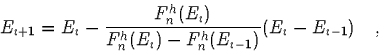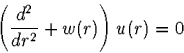
Um Differentialgleichungen der Form
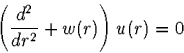 |
(5) |
zu lösen, kann man sich des Numerov-Verfahrens bedienen.
Wie auch beim Runge-Kutta Verfahren werden Differentialquotienten durch
Differenzenquotienten ersetzt, der lokale Fehler ist beim Numerov-Verfahren
jedoch von der Ordnung ![]() in der Schrittweite h und damit zwei
Ordnungen höher als das Verfahren nach Runge-Kutta.
in der Schrittweite h und damit zwei
Ordnungen höher als das Verfahren nach Runge-Kutta.
Vergleicht man obige Differentialgleichung mit der modifizierten radialen Schrödingergleichung (4), so findet man
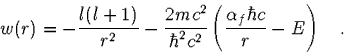
Durch die Diskretisierung der möglichen Werte von ![]() in Schritte der Länge h
kann man den Differentialquotienten in Gleichung (5) durch
einen Differenzenquotienten ersetzen.
Weiters wird die Lösung u(r) in ihre Taylorreihe entwickelt und erst nach
Gliedern 6. Ordnung abgebrochen.
Ebenso wird w diskretisiert durch
in Schritte der Länge h
kann man den Differentialquotienten in Gleichung (5) durch
einen Differenzenquotienten ersetzen.
Weiters wird die Lösung u(r) in ihre Taylorreihe entwickelt und erst nach
Gliedern 6. Ordnung abgebrochen.
Ebenso wird w diskretisiert durch ![]() .Unter Berücksichtigung der speziellen Struktur der Differentialgleichung
(5) erhält man eine Rekursionsbeziehung für diskrete Werte der Lösung:
.Unter Berücksichtigung der speziellen Struktur der Differentialgleichung
(5) erhält man eine Rekursionsbeziehung für diskrete Werte der Lösung:
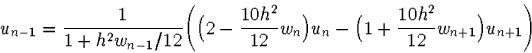
Die Lösung ![]() findet man schrittweise mit obiger Formel,
wobei man für den Iterationsanfang die asymptotische Lösung der radialen
Schrödingergleichung gemäß Gleichung (3) verwendet.
findet man schrittweise mit obiger Formel,
wobei man für den Iterationsanfang die asymptotische Lösung der radialen
Schrödingergleichung gemäß Gleichung (3) verwendet.
Eine physikalische Randbedingung für die Wellenfunktion ist, daß sie am Ursprung regulär sein muß. Das Coulombpotential besitzt am Ursprung jedoch eine Singularität, weshalb w(0)=w0 nicht ausgewertet werden kann. Dieses Problem wird umgangen indem man nur die rechte Gleichung in der Beziehung
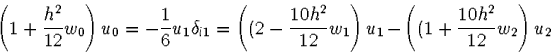 |
(6) |
Nachdem ausgehend von zwei Energien zwei Wellenfunktionen un(rn) berechnet wurden, kann mittels eines einfachen Newton-Verfahrens ein neuer Energieeigenwert bestimmt werden. Dazu wird die Bedingung für die Regularität der Wellenfunktion, Gleichung 6, benützt. Diese ist genau an den Nullstellen der Funktion
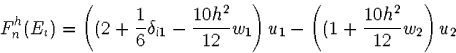 |
(7) |