Die Schrödingergleichung des Wasserstoffatoms

Das wellenmechanische, nichtrelativistische Modell Erwin Schrödingers ermöglicht es, das Wasserstoffatom mathematisch zu beschreiben und eine sehr gute Näherung für die Energieeigenwerte des Elektrons im Coulombfeld des Protons zu berechnen.

Dazu geht man von der Schrödingergleichung

$$i \hbar \frac{\partial}{\partial t}\psi(\vec r, t)=\frac{\hbar^2}{2m} \Delta\psi(\vec r, t)$$

aus. Da zeitunabhängige Lösungen gesucht sind, versucht man mit einem Separationsansatz zeit- und ortsabhängige Teile zu trennen und stationäre Wellenfunktionen zu finden. Den verbleibenden ortsabhängigen Teil trennt man weiter in eine winkelabhängigen Anteil und den Radialteil, der zur Lösung des Problems herangezogen wird. Die Separation der Schrödingergleichung führt für letzteren zu folgender Differentialgleichung:

 

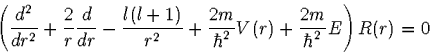$$\left(\frac{d^2}{dr^2}+\frac{2}{r}\frac{d}{dr}-\frac{l(l+1)}{r^2}+ \frac{2m}{\hbar^2}V(r)+\frac{2m}{\hbar^2}E\right) R(r)=0$$ (1)

Da es sich beim Wasserstoffatom um ein Zweikörperproblem handelt, muß für m die reduzierte Masse von Proton und Elektron eingesetzt werden. Diese ergibt sich zu $9,104\cdot 10^{-31}$ kg. Die entsprechende Ruheenergie beträgt rund $510\,721$ eV. Für das Potential V(r) setzt man das Coulompotential des Protons $V(r)=e_0^2/4\pi\varepsilon_0r$ ein. Die Separationskonstante l kann als Drehimpulsquantenzahl des Elektrons interpretiert werden und E als Gesamtenergie des Elektrons.

Eine genauere Untersuchung der radialen Schrödingergleichung zeigt, daß man analytische Lösungen von der Form

 

$$R(x)=A_l x^l L_n^{(2l+1)}(x) \exp(-x/2)$$ (2)

erhält. A_l ist eine Normierungskonstante, die die Interpretation von $\vert u_l\vert^2$ als Aufenthaltswahrscheinlichkeit ermöglicht, indem sie die Wellenfunktion auf 1 normiert. L sind die Laguerre-Polynome, die gemäß

$$L_n^{(m)}(x)=\sum_{k=0}^{n}\frac{n!}{(n-k)!}\frac{(n+m)!}{(m+k)!} \frac{(-x)^k}{k!}$$

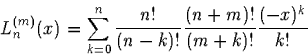
definiert sind. Die asymptotische Lösung ist

 

$$R(r)\propto \exp\left(-r\sqrt{-2mE/\hbar^2}\right)\quad.$$ (3)

Um die Differentialgleichung (1) einer numerischen Behandlung leichter zugänglich zu machen, formt man sie ein wenig um. Das Ziel ist es, möglichst einfache Ausdrücke zu erhalten, die etwa von der Größenordnung 1 sind, damit bei Summationen möglichst wenige Mantissenstellen verlorengehen und keine Auslöschungseffekte auftreten. Dazu wird eine neue Funktion u_l(r)=r R(r) definiert und einige Summanden der daraus folgenden Differentialgleichung mit c² erweitert:

 

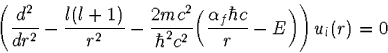$$\left(\frac{d^2}{dr^2}-\frac{l(l+1)}{r^2}- \frac{2mc^2}{\hbar^2c^2} \biggl(\frac{\alpha_f\hbar c}{r}-E\biggr) \right) u_l(r)=0$$ (4)

Als ,,natürliche`` Einheiten bei der Untersuchung des Wasserstoffatoms eignen sich Elektronvolt als Einheit der Energie und Nanometer als Einheit der Länge. Für mc² kann man somit $0.510720917212\cdot 10^6$ eV einsetzen und $\hbar c$ ergibt sich zu 197,327054065 eVnm. Die Sommerfeldsche Feinstrukturkonstante $\alpha_f$ hat den Wert 1/137,0359895.