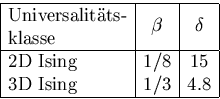Grundlagen

Spin-1/2-Ising-Modell

Beim Spin-1/2-Ising-Modell wird angenommen, daß sich Spins s_i an den Gitterplätzen eines Kristallgitters, das dem zu simulierenden Material entspricht, befinden. Nimmt man die Spinquantenzahl mit l=1/2 an, dann können die Spins lediglich 2l+1=2 Zustände $s_l=\pm 1$ haben. Die Hamiltonfunktion dieses Systems hat die Form  

$$H=-\sum_{{i,j} \atop {i \neq j}} J_{ij} s_i s_j - H_{ext} \sum_{i} s_i .$$ (1)

Die erste Summation erstreckt sich theoretisch über das gesamte Gitter, praktisch werden jedoch nur Wechselwirkungen zwischen nächsten Nachbarn angenommen. Nimmt man weiters an, daß die Wechselwirkungen für alle nächsten Nachbarn konstant sind, so reduziert sich J_ij auf ein Skalar J. Im Fall J>0 führt die parallele Ausrichtung der Spins zu einer Reduzierung der Energie und wird daher bevorzugt, sodaß es zu ferromagnetischem Verhalten kommt. Ist J=0, dann verschwindet die Wechselwirkung zwischen den Spins und man erhält paramagnetisches Verhalten. Ist schließlich J<0, so wird antiparallele Ausrichtung benachbarter Spins favorisiert und damit antiferromagnetisches Verhalten hervorgerufen.

Mittelwertbildung

Um thermodynamische Erwartungswerte zu bestimmen, wird beim Monte-Carlo-Verfahren der Konfigurationsraum entlang eines Zufallspfads (,,random walk``) abgetastet. Das Phasenraumintegral des kanonischen Ensembles

$$\langle A \rangle =\frac{\int A(z) \exp(-\beta H(z)) dz} {\int \exp(-\beta H(z)) dz}$$

wird durch einen stochastischen Mittelwert ersetzt.

$$\langle A \rangle =\frac{\sum_{\{z\}} A(z) \exp(-\beta H(z))} {\sum_{\{z\}} \exp(-\beta H(z))}$$

Werden alle Phasenraumpunkte z gleich gewichtet, so wird das als ,,direct sampling`` bezeichnet. Dabei werden jedoch auch nicht repräsentative Phasenraumpunkte berücksichtigt. Beim ,,importance sampling`` werden diese nicht zufällig ausgewählt, sondern entsprechend einer Wahrscheinlichkeitsverteilung P(z).

$$\langle A \rangle =\frac{\sum_{\{z\}} A(z) P^{-1}(z) \exp(-\beta H(z))} {\sum_{\{z\}} P^{-1}(z) \exp(-\beta H(z))}$$

Markov-Kette

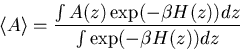
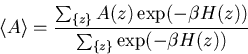
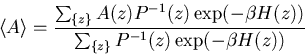
Einen Zufallspfad, der eine Folge von Punkten $\{z\}$ im Phasenraum auswählt, die gemäß P(z) verteilt sind, kann man durch einen Markov-Prozeß erzeugen. Nach Metropolis verwendet man die Wahrscheinlichkeit für einen Übergang von einem Zustand z zu einem Zustand z'  

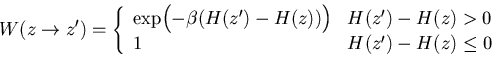$$W(z \to z')= \left\{ \begin{array} {ll} \exp\Bigl(-\beta ... ...H(z')-H(z) \gt 0 \\ 1 & H(z')-H(z) \leq 0 \end{array} \right.$$ (2)

und erhält damit eine Markov-Kette, die gegen die Gibbssche Verteilung $\exp(-\beta H(z))$ konvergiert.

Der Ensemble-Mittelwert kann dann durch einen Mittelwert über die Markov-Kette ersetzt werden

$$\langle A \rangle \simeq \bar A = \frac{1}{n} \sum_{i=1}^{n} A(z_i) ,$$

der sich mit geringerem Aufwand berechnen läßt.

Berechnung der thermodynamischen Größen

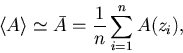
Aus der Energie und der Magnetisierung lassen sich die spezifische Wärme und die Suszeptibilität entsprechend dem Fluktuations-Dissipations-Theorem durch folgende Ausdrücke bestimmen:

$$C=\frac{\langle E^2 \rangle - \langle E \rangle^2}{k_B T^2}$$

und

$$\chi=\frac{\langle M^2 \rangle - \langle \vert M \vert \rangle^2}{k_B T}$$

Zur Bestimmung der kritischen Temperatur kann man die Divergenzen der spezifischen Wärme oder der Suszeptibiliät heranziehen. Einfacher ist es, den Kumulanten vierter Ordnung

$$U_L=1-\frac{\langle M^4 \rangle_L}{3 \langle M^2 \rangle^2_L}$$

zu verwenden. Bestimmt man diesen als Funktion der Temperatur für verschieden große Simulationszellen bei gleicher Schichtanzahl, so schneiden sich diese Kurven bei der kritischen Temperatur.

Randbedingungen

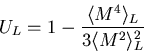
Reale Systeme enthalten größenordnungsmäßig 10²³ Teilchen, wir haben Monte-Carlo-Simulationen mit bis zu $32 \cdot 32 \cdot 10=1024$ Teilchen durchgeführt. Daraus ergibt sich das Problem, daß das Verhältnis von Oberfläche zu Volumen des Systems in Computersimulationen wesentlich größer ist als in realen Systemen. Um Oberflächeneffekte zu reduzieren, kann man periodische Randbedingungen verwenden. Dadurch wird ein ,,unendlich`` großes Gitter aufgebaut und Oberflächeneffekte werden vermieden. Das System muß aber ein ausreichende Größe aufweisen, um auch unerwünschte Effekte durch die Periodizität des Gitters zu verhindern.

Kritische Exponenten

In Experiment und Theorie wird bei $T \approx T_c$, also in der Nähe eines Phasenübergangs, beobachtet, daß gewisse physikalische Größen Potenzgesetzen gehorchen. Die entsprechenden Exponenten werden als ,,kritische Exponenten`` bezeichnet. Sie sind zu einem hohen Grad universell, d.h. nur von wenigen fundamentalen Parametern, wie etwa der Dimension des Systems, abhängig. Damit lassen sich Universalitätsklassen definieren. Für die Magnetisierung in Abhängigkeit von der Temperatur findet man das Gesetz  

$$M \sim (T_c-T)^\beta \qquad T<T_c .$$ (3)

Bei der kritischen Temperatur gilt für die Magnetisierung in Abhängigkeit vom äußeren Feld  

$$H \sim \vert M \vert^\delta \mbox{ sgn}(M) .$$ (4)

Für Spin-1/2-Ising Modelle sind folgende kritische Exponenten zu erwarten:

$$\begin{array} {\vert l\vert c\vert c\vert} \hline \mbox{Un... .../8 & 15 \\ \mbox{3D Ising} & 1/3 & 4.8 \\ \hline \end{array}$$