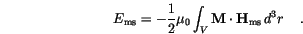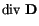 |
 |
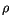 |
(2.6) |
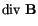 |
 |
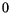 |
(2.7) |
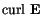 |
 |
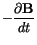 |
(2.8) |
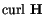 |
 |
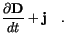 |
(2.9) |
The origin of domains still cannot be explained by the two energy terms above. Another contribution comes from the magnetostatic self-energy, which originates from the classical interactions between magnetic dipoles. For a continuous material it is described by Maxwell's equations
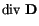 |
 |
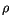 |
(2.6) |
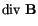 |
 |
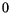 |
(2.7) |
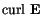 |
 |
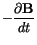 |
(2.8) |
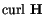 |
 |
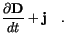 |
(2.9) |
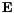 or free currents
or free currents 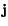 . Thus, there are two remaining equations
. Thus, there are two remaining equations
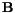 is given by
is given by
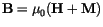 . A general solution of (
. A general solution of (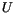 is the magnetic scalar potential. Inserting the expressions for
is the magnetic scalar potential. Inserting the expressions for 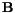 and
and 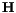 in (
in (
These equations have to be solved with the boundary conditions
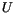 and derive from it
and derive from it 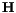 .
.  is the unit normal to the magnetic body, taken to be positive in outward direction.
is the unit normal to the magnetic body, taken to be positive in outward direction.
In micromagnetics, the magnetization distribution
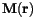 is given. With relation (
is given. With relation (![]() ) the magnetic scalar potential can be calculated from the magnetization distribution. The demagnetizing field
) the magnetic scalar potential can be calculated from the magnetization distribution. The demagnetizing field
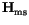 is then obtained by using (
is then obtained by using (![]() ).
).
Finally the magnetostatic energy is given by