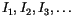 , each between 0 and
, each between 0 and 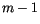 by the recurrence relation
by the recurrence relation
Many computer systems are supplied with random number generators in their standard libraries. These are usually linear congruential pseudo-random number generators [41], which generate a sequence of integers
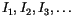 , each between 0 and
, each between 0 and 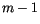 by the recurrence relation
by the recurrence relation
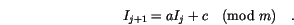
 and the increment
and the increment 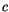 are positive integers and the modulus
are positive integers and the modulus 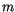 is a large number. If these three parameters are properly chosen, the sequence will be of maximal length, that is of length
is a large number. If these three parameters are properly chosen, the sequence will be of maximal length, that is of length 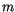 . In that case, all integers between 0 and
. In that case, all integers between 0 and 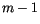 appear, before the sequence is repeated. Thus, any initial seed
appear, before the sequence is repeated. Thus, any initial seed  is as good as any other. In order to have a uniform distribution in the interval
is as good as any other. In order to have a uniform distribution in the interval  , generally
, generally 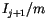 is returned. It is clear from the recursive form, that
is returned. It is clear from the recursive form, that 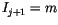 cannot occur and therefore
cannot occur and therefore 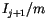 is strictly less than 1.
is strictly less than 1.
The quality of this random number generator depends only on the parameters in the recurrence relation, and it is satisfactory for many applications, but far from perfect. For example, successive numbers differ by a multiple, which is orders of magnitude smaller than the modulus. These low-order correlations are removed by shuffling the output. A random deviate derived from the 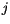 th value in the sequence,
th value in the sequence, 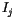 , is output not on the
, is output not on the 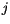 th call, but rather on a randomized later call.
th call, but rather on a randomized later call.
If even longer random sequences are needed, two different sequences can be combined to obtain a new sequence, whose period is the least common multiple of the two periods. When implementing a random number generator, special care must be taken of the machine's maximum value for an integer number and the size of the mantissa in the floating-point representation.
Thus, the quality of a random number generator should only be limited by its period.