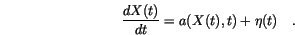
For simplicity let us assume a one dimensional stochastic differential equation with additive noise [41]
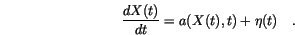
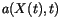 in this Langevin equation can be interpreted as a deterministic or averaged drift term perturbed by a noisy diffusive term
in this Langevin equation can be interpreted as a deterministic or averaged drift term perturbed by a noisy diffusive term 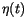 which is a Gaussian random variable.
which is a Gaussian random variable.
For the increase 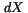 during a time step
during a time step 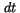 we get (to first order)
we get (to first order)
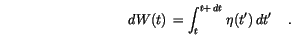
 is a Gaussian random variable, because it is the sum of Gaussian random variables.
Thus,
is a Gaussian random variable, because it is the sum of Gaussian random variables.
Thus,

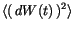 |
 |
 |
(6.6) |
 |
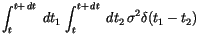 |
(6.7) | |
 |
 |
(6.8) |
![$[t,t+\,d{t}\,]$](img241.gif) and
and
![$[t',t'+\,d{t}\,]$](img242.gif) do not overlap, which is true for successive time steps, we get
do not overlap, which is true for successive time steps, we get
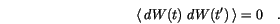
It should be emphasized, that only the second moment of  is linear in
is linear in 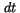 .
.  is only of the order of
is only of the order of 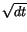 . This important aspect is made clear by writing
. This important aspect is made clear by writing

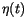 denotes a Gaussian random variable.
denotes a Gaussian random variable.