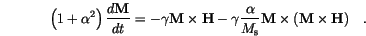 is given by the rate of change of angular momentum
is given by the rate of change of angular momentum  with time
with time
The solution of Brown's equations gives us the magnetization distribution in equilibrium. If we are interested in the dynamic properties and time evolution of the magnetization, we have to consider the precession of the magnetization in a magnetic field [16].
The torque 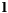 is given by the rate of change of angular momentum
is given by the rate of change of angular momentum  with time
with time
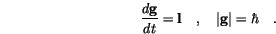
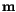 in a magnetic field
in a magnetic field 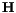 is given by
is given by

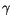

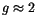 is the Landé factor,
is the Landé factor, 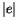 the elementary charge, and
the elementary charge, and 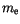 the electron's mass. The magnetic field constant
the electron's mass. The magnetic field constant 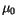 has been pulled into
has been pulled into 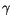 . By the above definition
. By the above definition 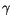 is positive, but the electron's charge is negative. As a result, we obtain
is positive, but the electron's charge is negative. As a result, we obtain
We can replace the magnetic moment of the electrons by the magnetization. The magnetic field, which drives the precession, can be identified with the effective field (![]() ), but we simply write
), but we simply write 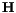 . Thus, we obtain
. Thus, we obtain
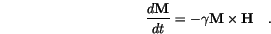
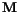 about the field direction. It is the well known Larmor precession with the Larmor frequency
about the field direction. It is the well known Larmor precession with the Larmor frequency
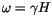 .
From experiments it is known, that changes in the magnetization decay in finite time. As this damping cannot be derived rigorously from basic principles, it is just added by a phenomenological term. In reality it is caused by a complex interaction of the electron's magnetic moment with the crystal lattice.
.
From experiments it is known, that changes in the magnetization decay in finite time. As this damping cannot be derived rigorously from basic principles, it is just added by a phenomenological term. In reality it is caused by a complex interaction of the electron's magnetic moment with the crystal lattice.
Gilbert [17] proposed a damping term of the form

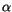 .
.
It is equivalent to a an older form of Landau and Lifshitz [18], which is usually written as
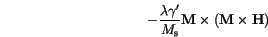
 .
.
The relationship between 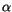 and
and  can be derived as follows. First, we apply
can be derived as follows. First, we apply
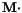 to both sides of the Gilbert equation
to both sides of the Gilbert equation


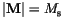 remains constant during the motion, as assumed in (
remains constant during the motion, as assumed in (
When we apply
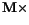 to both sides of Gilbert's equation (
to both sides of Gilbert's equation (![]() ), we get
), we get
 |
 |
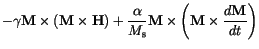 |
|
 |
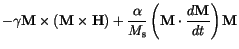 |
||
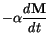 |
|||
 |
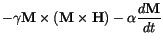 |
(2.23) |
If we substitute this result in (![]() ), we arrive at
), we arrive at