


Next: 4.2.1 Preconditioning
Up: 4. Solution of the
Previous: 4.1 Energy Minimization
Contents
4.2 The Dynamic Equation
The Landau-Lifshitz-Gilbert equation (Eq. (3.8)) is a system of ordinary differential equations (ODEs), which can be written in a general form as
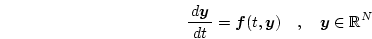 |
(4.7) |
with the initial condition
 |
(4.8) |
The PVODE package [48,49] is a general purpose solver for initial-value problems for stiff and non-stiff ODEs of the form of Eq. (4.7). It is based on CVODE [50,51] and uses MPI for parallelization and portability.
Two methods are available for the numerical solution of Eq. (4.7): The backward differentiation formula (BDF), which is recommended for stiff problems, and the Adams-Moulton formula for non-stiff problems, both of which feature a variable stepsize and variable order. Both formulas can be written as the linear multistep formula
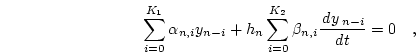 |
(4.9) |
where
 is the stepsize and
is the stepsize and 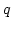 the order. The Adams-Moulton formula is obtained with
the order. The Adams-Moulton formula is obtained with 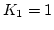 and
and 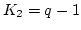 with
with
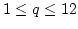 . The BDF formula is represented by Eq. (4.9) with
. The BDF formula is represented by Eq. (4.9) with 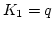 and
and 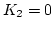 with
with 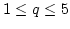 . The numerical integration is started with
. The numerical integration is started with 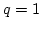 and then varied automatically and dynamically.
and then varied automatically and dynamically.
If we insert Eq. (4.7) in Eq. (4.9) we get an implicit nonlinear system of equations for
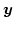
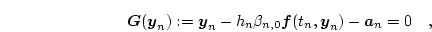 |
(4.10) |
which has to be solved at each time step. 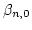 and
and
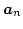 depend on the method, the integration order, and the previous time steps. An efficient method for nonstiff problems is functional iteration, because it does not require the solution of a linear system of equations. However, for stiff problems it is better solved by Newton iteration, which does involve the solution of a linear system of equations. PVODE uses a Krylov subspace method - the iterative scaled preconditioned generalized minimal residual method (SPGMR) [52], whose performance can be considerably improved with suitable preconditioners.
depend on the method, the integration order, and the previous time steps. An efficient method for nonstiff problems is functional iteration, because it does not require the solution of a linear system of equations. However, for stiff problems it is better solved by Newton iteration, which does involve the solution of a linear system of equations. PVODE uses a Krylov subspace method - the iterative scaled preconditioned generalized minimal residual method (SPGMR) [52], whose performance can be considerably improved with suitable preconditioners.
Subsections



Next: 4.2.1 Preconditioning
Up: 4. Solution of the
Previous: 4.1 Energy Minimization
Contents
Werner Scholz
2003-06-08
![]()