Error estimation, refinement and interpolation

  For the refinement of the finite element grid certain elements have to be selected and split into smaller elements as described in section 3. The selection is based on an estimated error, which is imported and stored in the data structure of the elements by the imperror command. The estimator has the task to decide which elements have to be refined. Currently five estimators are available.

The user can choose one of them by setting the variable estimator to the appropriate name. The tolerance has a different meaning for each estimator. Its default value 0.5 can be changed using the variable tolerance. If estimate is invoked without any arguments the value stored in the variable tolerance will be handed over to the estimator. Else the value given as an argument will override the variable tolerance. estimate invokes the estimator specified by estimator, which will mark all elements necessary. If an irregular element would be selected, its father is marked for regular refinement, because Bey's refinement algorithm prohibits an irregular element being refined.

• markall estimator

  All leaf (i.e. unrefined) elements will be marked for regular refinement. The command mark all provides a more convenient way to refine the whole grid.

• abs estimator

  All elements whose error is greater than the given tolerance will be marked.

• etamax estimator

  If the error 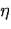$\eta$ of an element of the finest triangulation complies with 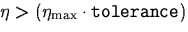$\eta \gt (\eta_{\mbox{\scriptsize max}} \cdot \mbox{\tt tolerance})$, it is marked for regular refinement.

• eps estimator

  Those elements for which 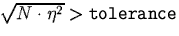$\sqrt{N \cdot \eta^2}\gt \mbox{\tt tolerance}$, where 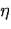$\eta$ is the error of the current element and N the total number of finite elements, is true, are marked for regular refinement.

• diff estimator

  First the difference between the two magnetization vectors at the ends of each edge of the current element is calculated. The length of each of these six difference vectors is computed and finally summed up. If the result is greater than the allowed tolerance the element is marked for refinement.

After execution of estimate the desired elements are marked for refinement. If too few or too many elements are marked or another estimator is chosen, estimate can be called again, which will first clear all marks and evaluate the elements' errors again.

The refinement itself can be effected by the command refine. It will insert all necessary elements and vertices. However, these newly inserted vertices contain no valid magnetization vector yet. It can be computed with interpolate (implemented in mga.c). This command interpolates linearly between the magnetization vectors at the ends of the edge which is bisected by the inserted vertex and stores the result in the new vertex. Finally, the length of the magnetization vector is changed to 1 if it is greater than 10^-20. Otherwise it remains unchanged, which leaves it in a rather unphysical state. The magnetization vector can be very short under two circumstances. Either the magnetization vectors that are used for the interpolation are of almost equal length and point in opposite directions or they are very short themselves.

In the first case the new vertex lies between two different domains in a domain wall. This could either be a Bloch wall (magnetization vector rotates in the plane of the wall) or a Néel wall. Since the interpolated vector is very short there is no ``domain wall'', rather a non-magnetized area. The second case should not occur since the length of all magnetization vectors computed by vecu have length 1.